If we know call option prices for every strike (underlying and expiry date being the same for all of the options), and the option price is a twice differentiable function of the strike, then we can calculate the probability density of the underlying on the expiry date. This density is implied by the option prices.
If C(K) is the price of the option with strike K, then the implied density of the underlying on expiry date is C”(K). Remarkably, this does not imply any particular model for the underlying process. This fact is well known, but I could not find a proof of it anywhere in the literature. To me, the following informal reasoning sounds pretty convincing.
Suppose we have a family of European call options on the same underlying S and the same expiry date T, with strikes K. The option price is a function of strike: C(K). If C is twice differentiable, then C”(K) is the probability density function of S(T) implied by the option prices. In other words, if we have a derivative whose pay-off is contingent only on S(T), then the price of this derivative is uniquely derived from C”(K). If  is the derivative’s pay-off function, then the derivative’s price V is given by
is the derivative’s pay-off function, then the derivative’s price V is given by

Informal proof
Firstly, we will show that the value of a binary option that pays 1 if S(T)>K and 0 otherwise is

Consider contract X that consists of a bought call option with strike K and a sold call option with strike (K+δ), and take 1/δ of X. The price of 1/δ*X is

and its pay-off is

If  then this pay-off tends to the pay-off of a binary option with strike K. At the same time the price of that contract tends to the negated derivative of C(K):
then this pay-off tends to the pay-off of a binary option with strike K. At the same time the price of that contract tends to the negated derivative of C(K):

by definition of the derivative. Therefore, the price of the binary option

Next, we will consider a contract with pay-off contingent on S(T):

and replicate this pay-off with binary options with different strikes. We choose a number ε and strikes

for i=0,1,…n.
Then we buy  of binary call with strike
of binary call with strike  (for each i=1,…n) and
(for each i=1,…n) and of binary call with strike 0. The figure below shows the pay-off of this combination of binary options as solid line, and
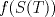 as dotted line.
as dotted line.

The cost of our sum of binary options will be


When  , the pay-off of the sum of binary options tends to
, the pay-off of the sum of binary options tends to . At the same time,
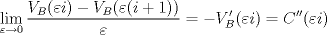
so the price of the sum of the binary options is actually

We notice that this is a Riemann sum for

Thus we saw that this integral is the limit of the value of the portfolio of binary options which pay-off tends to . This means that C” represents the probability density of S(T) implied by the option prices.
The above reasoning lacks mathematical rigor, but it shows how one can construct a portfolio that replicates a contingent claim with arbitrary pay-off .